Om maar meteen met de deur in huis te vallen: een goede journalist kan rekenen. Want een journalist die niet kan rekenen, is eenvoudig te misleiden. En dat is precies wat je niet wilt, als waarheidsvinding zo’n belangrijk onderdeel van je vak is.
In essentie draait journalistiek om verificatie - dat geldt voor alle bronnen, dus ook voor cijfers en tabellen. Vanzelfsprekend betekent dit dat je ook voor cijfers moet uitzoeken of de bron betrouwbaar is en de informatie juist en volledig is. Bij het controleren en interpreteren van cijfers, helpt het vaak om een voorbeeld te nemen om te zien of je het werkelijk begrijpt.
Misschien ben je wel journalist geworden omdat de journalistiek ‘zo lekker alpha’ is, en de bèta-vakken ‘niet aan jou besteed waren’. Wij begrijpen het. Maar het verschil tussen ‘goed met cijfers’ en ‘getallen zijn niet m’n ding’ is werk.
Wij zijn er om jou, zo snel en zo luchtig mogelijk, met dit essentiële werk te helpen. Ga er lekker voor zitten - kopje koffie erbij? - en leer de basisprincipes van cijfers op Als Het Ongeveer Maar Klopt. De totale leestijd is zo’n dertig á veertig minuten, verdeeld over vijf hoofdstukken. Mocht je daar geen tijd voor hebben, download dan hier de samenvatting van Als Het Ongeveer Maar Klopt (PDF).
Let op: de kans bestaat dat je van AHOMK cijferwijzer wordt. Verder lezen is op eigen risico.
Veel plezier!
Lars en Winny
01 Verandering
Onze liefde voor cijfers is net iets groter dan onze liefde voor pizza. Als je met elkaar een pizza eet, verdeel je de pizzapunten: Lars drie pizzapunten, Winny drie pizzapunten en als je aardig bent twee voor jou. Soms zijn verdelingen nieuwswaardig: bijvoorbeeld als het over de zetels in de Tweede Kamer gaat, of over bedragen uit de begroting.
Er volgen nu een paar rekenvoorbeelden, maar schrik niet: we beloven je dat we de voorbeelden zo goed en helder mogelijk uitleggen.
Dit is echt puur hypothetisch: onze pizza’s eten we zelf wel op.
Breuken en percentages
Elke verdeling is in feite een breuk, en elke breuk is een percentage. Stel dat we onze pizza met jou delen. Als we jou twee van de acht pizzapunten geven, krijg je 2/8e deel.
Omdat je wel aardig bent, maar niet zó aardig; staat de teller op twee. Je krijgt maar twee punten van de acht pizzapunten in totaal. Het totaal aantal delen, acht in dit geval, noemen we de noemer.
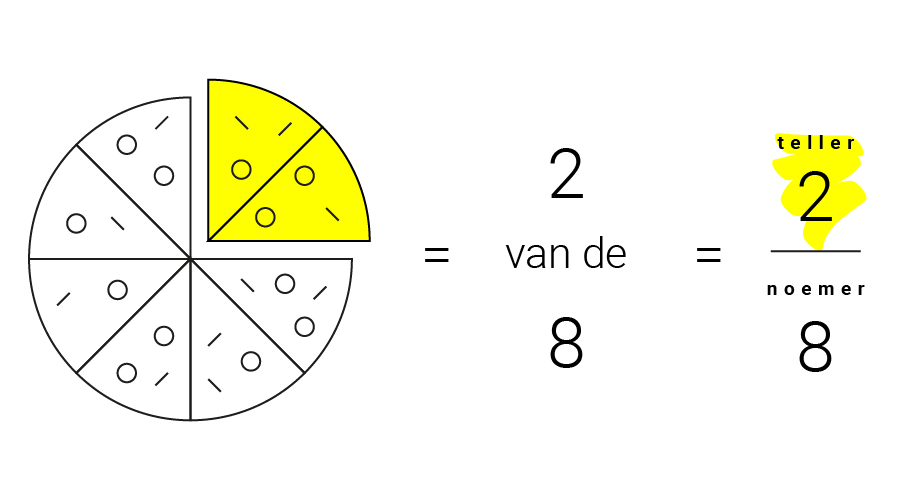
Een percentage is een breuk waarvan de noemer 100 is. Procent betekent namelijk 'per honderd'. Om uit te rekenen hoeveel procent van onze pizza jij krijgt, moet je 2/8 omzetten naar ?/100. Omdat honderd gedeeld door acht 12,5 is; weten we dat acht keer 12,5 honderd is. Om van acht naar honderd te gaan, moet je dus vermenigvuldigen met 12,5.
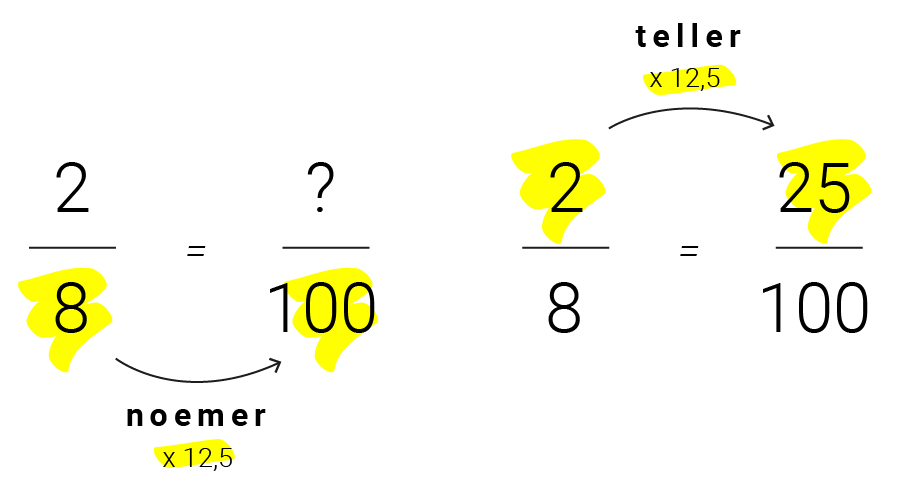
Dit doe je ook bij de teller. Twee van de acht punten is net zo veel als 25 van de honderd punten. En 25 per honderd is gelijk aan 25 procent.
De berekening waarmee je een deel van het geheel omzet in een percentage, is vaak het hart van journalistieke verhalen over nieuwe verdelingen. Denk bijvoorbeeld aan verkiezingen: het nieuws zit in de herverdeling van de zetels in het parlement.
Tijdens de Tweede Kamerverkiezingen in 2017 kreeg de Partij van de Arbeid negen zetels van de 150 kamerzetels in totaal. Dit deel van het geheel zou je als breuk opschrijven als 9/150.
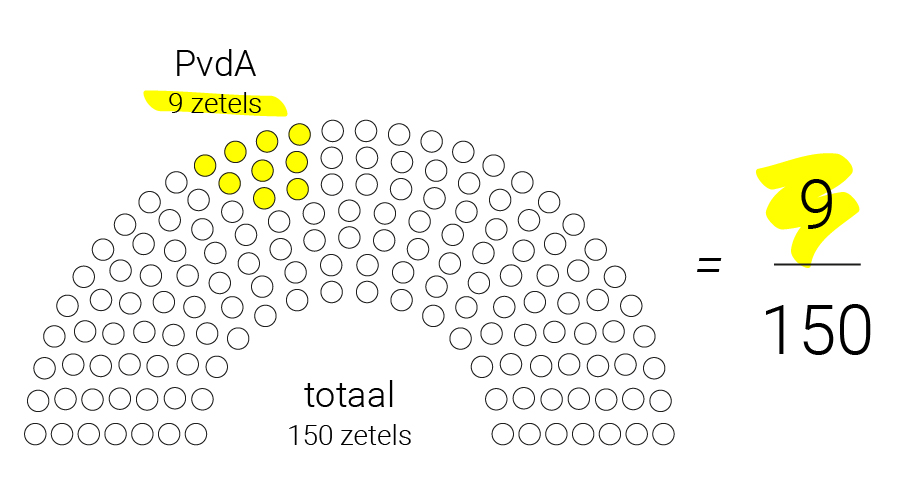
Met 150 als noemer, wordt het al lastiger om de noemer om te zetten naar 100. Je kunt daarom een ezelsbruggetje gebruiken.
tl;dr
Deel van het geheel
Hoeveel procent is een deel van het geheel?
Berekening: (Deel / Geheel) x 100%
Terug naar ons voorbeeld: de Partij van de Arbeid kreeg 9 van de 150 zetels. Hoeveel procent is dat?
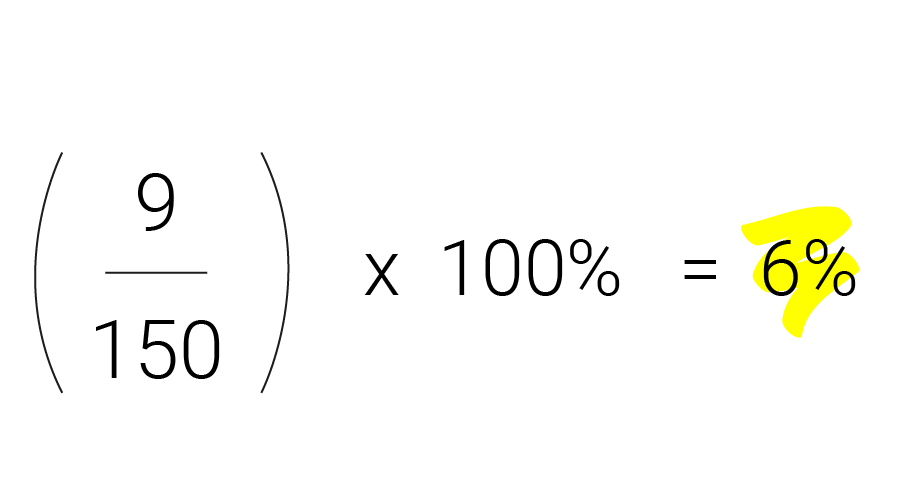
De PvdA haalde niet eerder zo weinig zetels. Dat maakt zes procent een nieuwswaardig getal. Maar het wordt nog interessanter, als je het in de context van de Nederlandse politieke geschiedenis bekijkt: als je kijkt naar de procentuele verandering.
Procentuele verandering
In 2012 werd de PvdA, achter de VVD, de op een na grootste partij van Nederland met 38 zetels. Bij de verkiezingen in 2017 behaalde de PvdA maar negen zetels. Nooit eerder was de partij zo klein - het aantal van negen was historisch laag en daarmee nieuwswaardig op zich. Maar ook de verandering - de val van 38 naar 9 zetels - heeft nieuwswaarde.
Op basis van deze absolute getallen - 38 zetels in 2012, negen zetels in 2017 - kun je eenvoudig een procentuele verandering berekenen. Hiervoor kun je de volgende breuk maken:
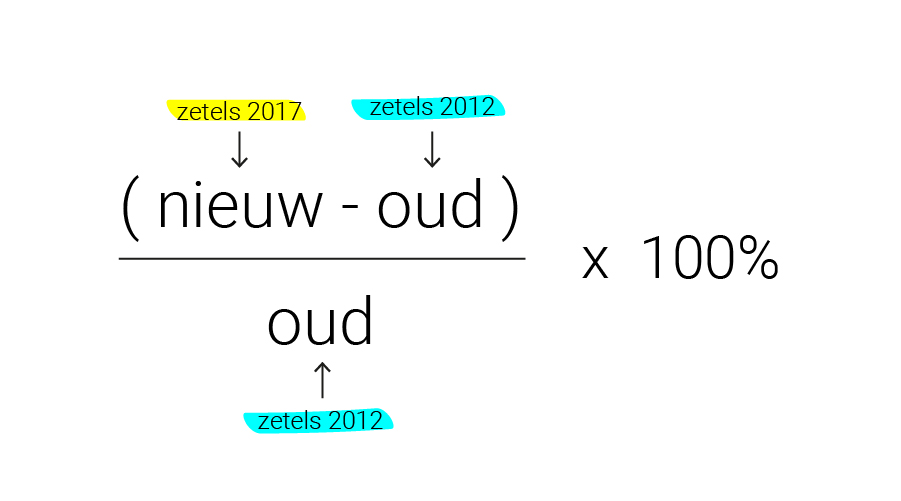
Voor het berekenen van de procentuele verandering van het aantal PvdA-zetels in de Tweede Kamer, krijg je de volgende som:
tl;dr
Procentuele verandering
Hoe bereken je een procentuele verandering?
Berekening: (Nieuw - Oud) / Oud) x 100%
Procenten vs procentpunten
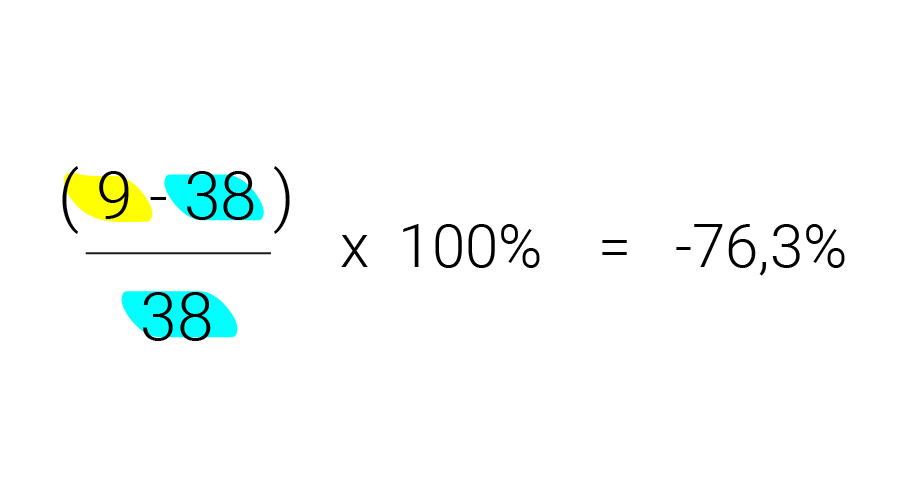
Je weet nu hoe je verandering kunt uitdrukken in procenten, maar wat als de aantallen al in percentages zijn uitgedrukt? Dan wordt het ingewikkeld:
‘De PvdA behaalde bij de verkiezingen in 2017 6 procent van de stemmen, 76 procent minder dan in 2012, toen de PvdA nog 25 procent van de stemmen haalde.’
Deze zin lijkt verwarrend. In de eerste plaats omdat de schrijver het voor elkaar krijgt om in één zin vijf getallen te noemen, maar er is nog iets aan de hand. Hoe kan er een verschil van 76% ontstaan, terwijl de percentages veranderen van 6% naar 25%?
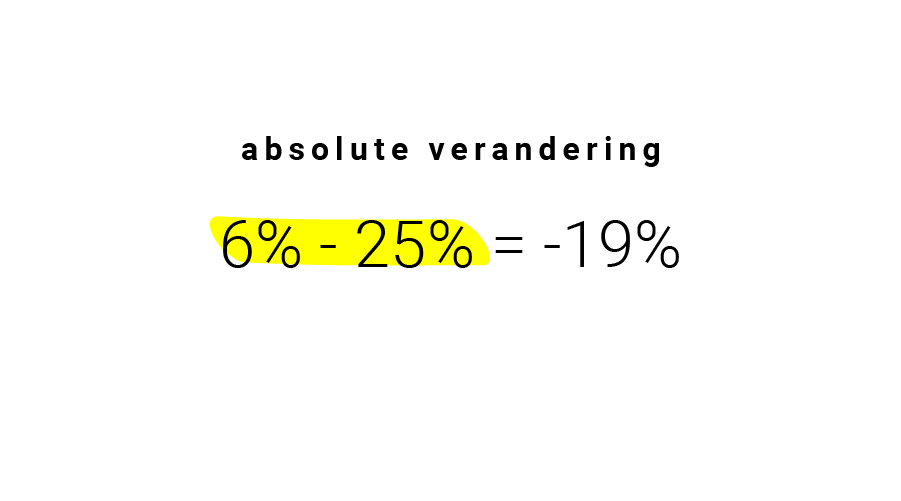
Met die som is niks mis, maar je ziet hier een absolute verandering, niet de procentuele verandering. Zoals je net hebt gelezen, bereken je die op een andere manier. Namelijk zo:
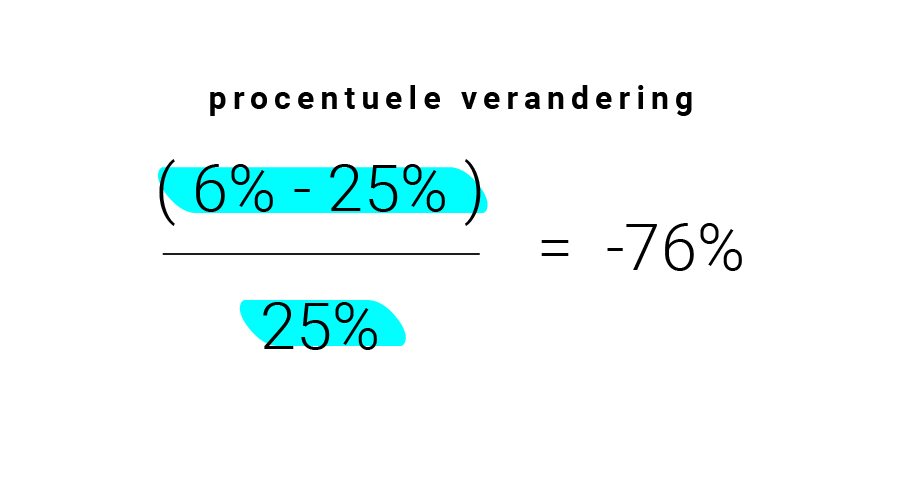
Als je percentages met elkaar wilt vergelijken, noem je de absolute verandering anders: procentpunt. Dit zou dus een minder verwarrende zin zijn:
‘De PvdA behaalde bij de verkiezingen in 2017 6 procent van de stemmen, 19 procentpunt minder dan in 2012, toen de PvdA nog 25 procent van de stemmen haalde.’
Je kunt je afvragen of we het hiermee voor de lezer duidelijker hebben gemaakt. De kans bestaat dat een lezer het verschil tussen procenten en procentpunten niet kent, maar dat is niet het punt.
Journalistiek is de business van waarheidsvinding, dus laten we de dingen noemen zoals ze zijn. Laten we procentpunten procentpunten noemen - en dus geen procenten. We adviseren dit niet omdat wij procentpunten nu zo mooi vinden, maar omdat procentpunten procenten noemen nu eenmaal onjuist is.
tl;dr
Procentpunten - procenten
Een absolute verandering tussen twee percentages druk je uit in procentpunten. Een relatieve verandering druk je uit in procenten.
Voorbeeld: Het verschil tussen zes procent en vijfentwintig procent is negentien procentpunt. De relatieve verandering is 76 procent.
Al vinden wij procentpunten natuurlijk wél prachtig!
Ongelijke getallen vergelijken
Met de deel van geheel-berekening kun je meer dan alleen percentages berekenen, je kunt er ook ongelijke getallen mee vergelijken. We blijven nog even bij de verkiezingsuitslag, maar we zoomen in naar lokaal niveau.
In 2017 kreeg de PvdA in Amsterdam 38.300 stemmen. Dat zijn er een stuk meer dan in Leeuwarden, waar 6.900 mensen op de PvdA stemden. Als je wilt bepalen waar de PvdA het grootst is, heb je niet zoveel aan deze absolute vergelijking. Het inwonertal in Amsterdam (863.000) is groter dan Leeuwarden (123.000). Als je de stemmen op de PvdA in Amsterdam met de PvdA-stemmen in Leeuwarden wilt vergelijken, moet je de uitslagen corrigeren voor de bevolking.
Of preciezer gezegd: corrigeren voor het aantal kiesgerechtigden, want niet iedere inwoner mag stemmen. En omdat stemmen in Nederland niet verplicht is, moet je de uitslag ook corrigeren voor de opkomst. Twee correcties, dat betekent twee berekeningen.
Om het je makkelijk te maken, hebben we alle relevante cijfers op een rijtje gezet:
Stad
Amsterdam
Leeuwarden
Aantal kiesgerechtigden
585.340
84.942
Aantal stemmen op PvdA
38.332
6.932
Opkomst
78,9%
80,7%
Met deze cijfers kunnen we onze vergelijking maken. We beginnen met de opkomst: het aantal stemmers (deel), ten opzichte van het aantal kiesgerechtigden (geheel).
In het geval van Amsterdam weten we de opkomst als percentage: 78,9% - van de 100 kiesgerechtigden, gingen er 78,9 naar de stembus. We weten ook hoeveel 100% is: namelijk 585.340 kiesgerechtigden. Wat wij willen weten is hoeveel 78,9% van 585.340 is.
In één berekening van 100 naar 78,9 vereist wat denkwerk. Maar we hebben geen haast, dus gaan we voor de makkelijke weg en doen we het in twee stappen. Let op:
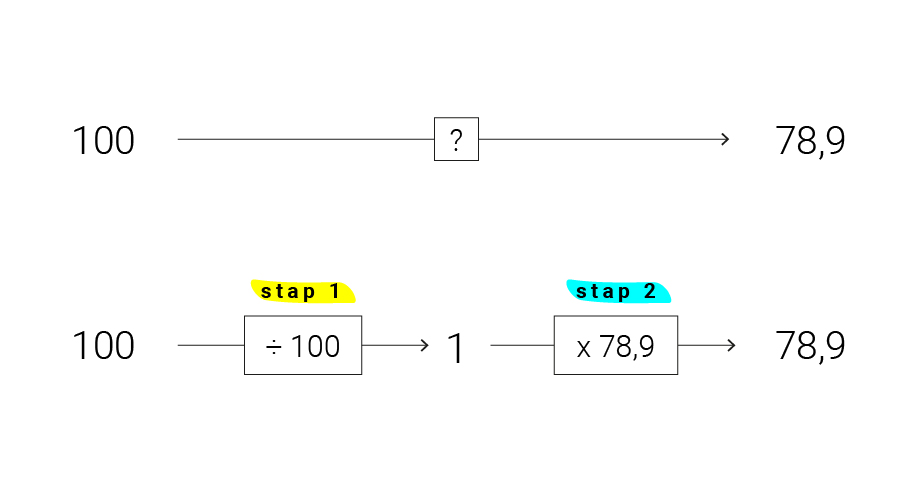
Om van 100 naar 78,9 te gaan, deel je eerst door 100 en vermenigvuldig je daarna met 78,9. Op diezelfde manier kunnen we nu ook berekenen hoeveel 78,9% van 585.340 is:
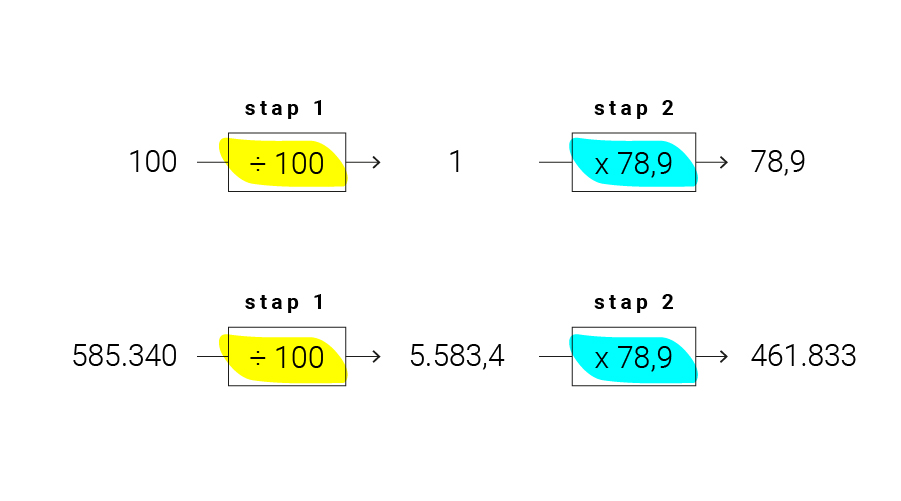
Dit doe je ook voor Leeuwarden:
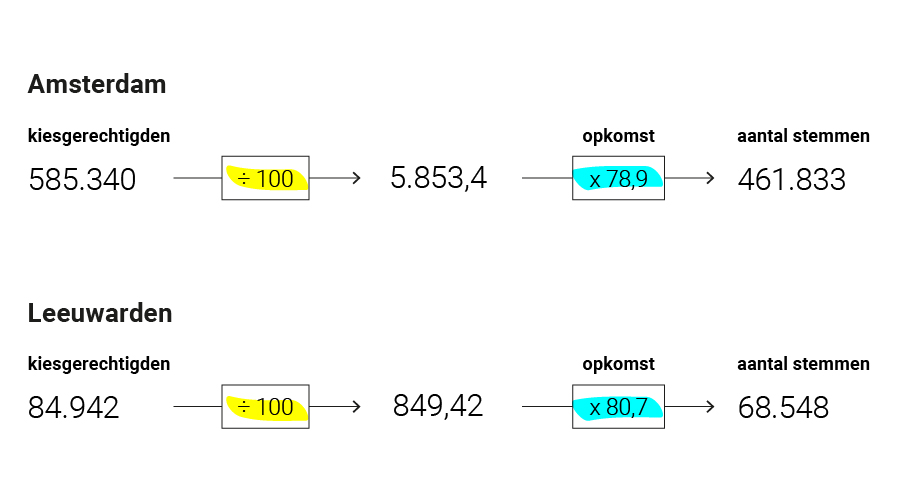
Beide uitslagen hebben we nu gecorrigeerd voor de opkomst. Nu gaan we de cijfers corrigeren voor de bevolking. Om Amsterdam en Leeuwarden te kunnen vergelijken, kijken we naar de uitslag per 1000 stemmen. Dit doe je eerst door het totaal aantal stemmen te delen door 1000.
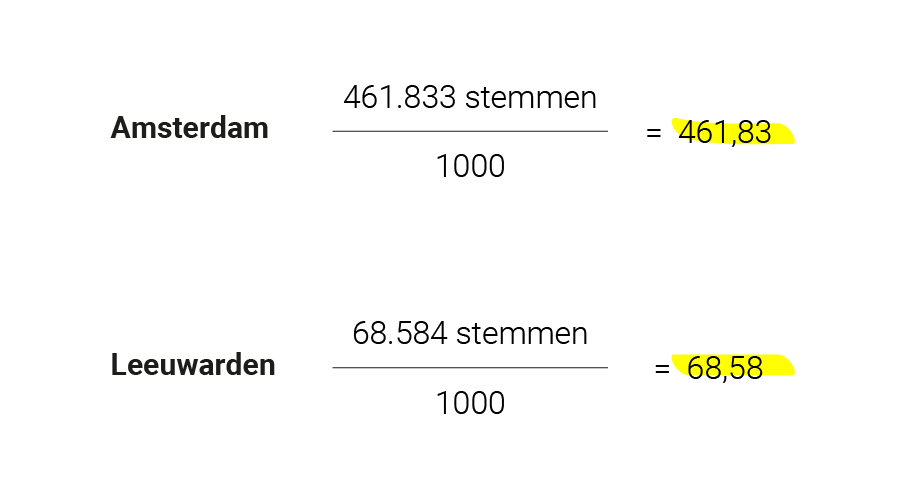
Om in Amsterdam 461.833 stemmen terug te brengen tot 1000, moet je het dus delen door 461,83. Voor Leeuwarden moet je het delen door 68,58. Dit doe je ook voor het aantal PvdA-stemmers, zodat je weet hoe die zich verhouden tot 1000 stemmen.
Van de 1000 stemmen waren er in Leeuwarden 101 voor de PvdA. In Amsterdam waren dat er 83 op de 1000. Doordat we de factor bevolking hebben weggenomen, zijn de getallen goed met elkaar te vergelijken.
tl;dr
Getallen vergelijken
Als je ongelijke getallen toch met elkaar wilt vergelijken, geldt de volgende vuistregel: alles wat je niet wilt vergelijken moet gelijk zijn, zodat je zeker weet dat je vergelijkt wat je wilt vergelijken.
In het vorige hoofdstuk legden we uit hoe je niet bang hoeft te zijn van getallen. Maar een paar getallen in een overzichtelijke tabel voelt toch heel anders dan een bestand met honderd, duizend of 1.048.576 getallen. We snappen dat je daarvan schrikt. In dit hoofdstuk vertellen we hoe jij een hele reeks cijfers angst aan kunt jagen in plaats van andersom.
Daarvoor moeten we je eerst blootstellen aan een rijtje cijfers. Komt 'ie:
Uitersten en het midden
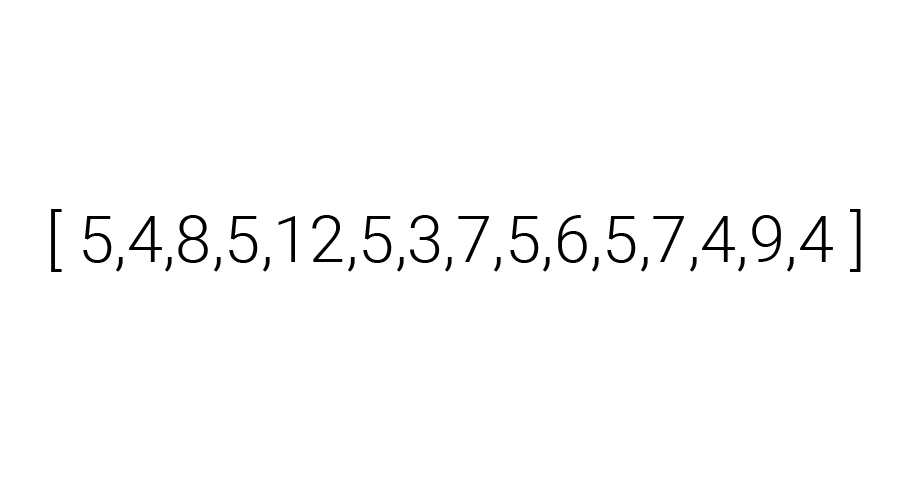
Stel jezelf gerust met de gedachte dat zelfs de grootste bèta deze getallenreeks niet in één oogopslag kan lezen. Om orde te scheppen in de getallenchaos, zetten we de cijfers op volgorde van laag naar hoog:
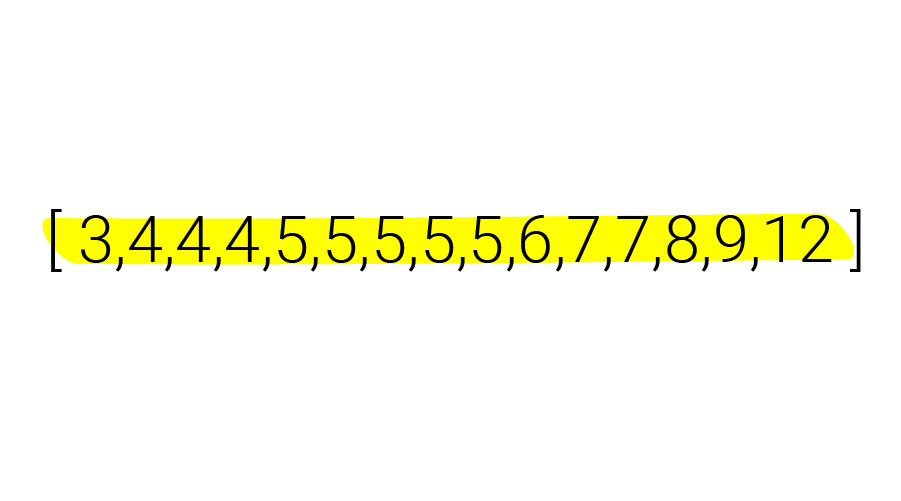
Dat maakt het lezen al wat makkelijker. Sterker nog, je hebt meteen overzicht over twee journalistiek relevante getallen: het minimum en het maximum.
Die uitersten zijn interessant, want journalistiek gaat vaak over dingen die afwijken. Maar voor je een afwijking kunt vaststellen, moet je weten welke getallen er tussen het minimum en maximum in zitten. Het midden is daarmee van een even groot journalistiek belang.
Dat midden, of ‘centrum’ zoals statistici liever zeggen, kun je op verschillende manieren bekijken. Wij leggen je de populairste manieren uit: het gemiddelde, de modus en de mediaan. In de statistiek heten dit ‘centrummaten’. Welke centrummaat het belangrijkst is, is afhankelijk van het verhaal dat je wilt vertellen.
tl;dr
Data doorgronden
Als je een getallenreeks op volgorde zet, zie je de uitersten. Om te bepalen of er uitschieters zijn, en om te zien hoe deze zich verhouden tot de rest; moet je kijken naar het centrum - de getallen tussen de uitersten in, en de centrummaten die daaruit voortvloeien.
Gemiddelde
Je berekent het gemiddelde door alle getallen in de reeks op te tellen, en daarna te delen door het aantal getallen in diezelfde reeks.
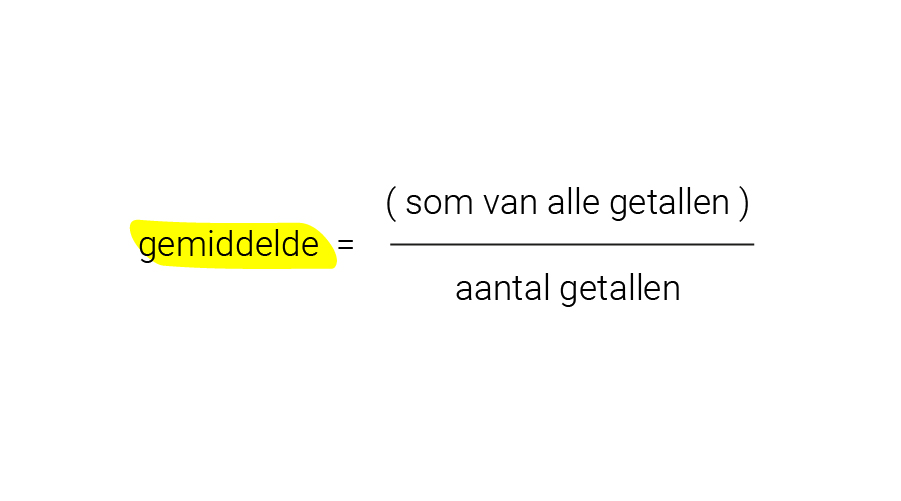
In onze getallenreeks, die uit vijftien cijfers bestaat, ziet dat er zo uit:
Als je het gemiddelde kent, kun je iets over de rest van de getallen in de reeks zeggen. Je kunt nu zien wanneer iets afwijkt van het gemiddelde. Met een eenvoudige som kun je ook uitrekenen hoe groot die afwijking is.
tl;dr
Het gemiddelde
Het rekenkundig gemiddelde bereken je door de som van alle getallen te delen door het aantal getallen.
Modus
tl;dr
De modus
De modus is het getal dat in je getallenreeks het vaakst voorkomt.
Je kunt de modus vinden, door de getallen te turven. Dat ziet er in onze getallenreeks er zo uit:
Het CPB heeft niet alle inkomens van Nederland geturfd, maar een rekensom gemaakt.
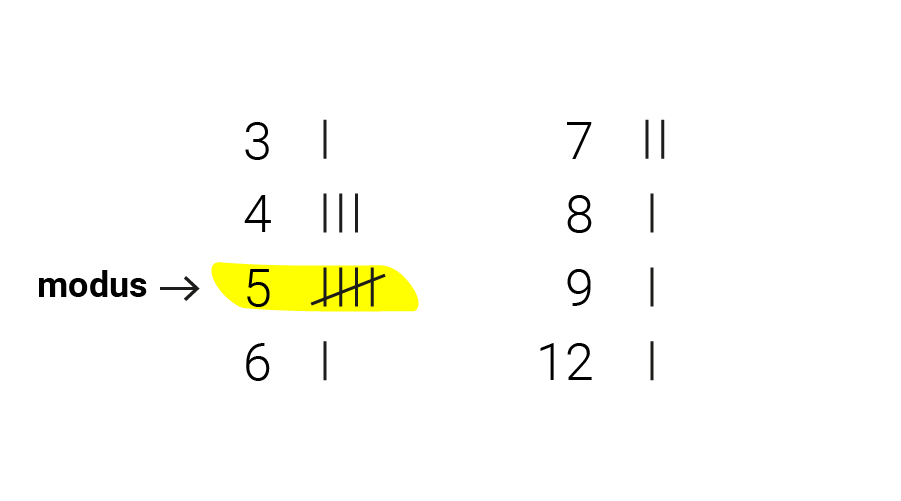
De modus laat zich niet zo vaak zien, maar je kunt ‘m in het wild tegenkomen, vermomd in onze spreektaal als ‘gemiddelde’. Zo wordt het modaal inkomen wel eens vertaald als het ‘gemiddelde inkomen’, maar strikt genomen is dat het niet. Het modale inkomen is de modus; het inkomen dat het vaakst verdiend wordt. Anders gezegd, het modale inkomen is het inkomen dat de meeste mensen verdienen.
Het verschil tussen het modale inkomen en het gemiddelde inkomen kun je goed zien in de grafiek hieronder.
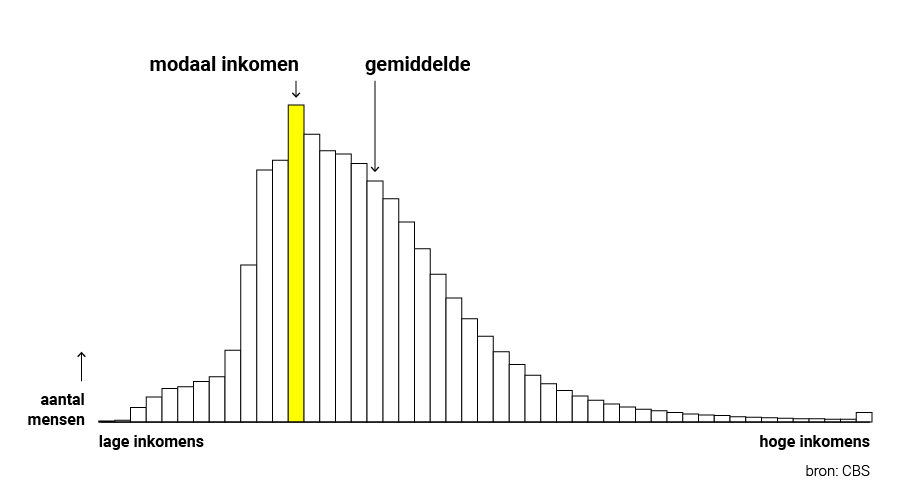
Het gemiddelde inkomen ligt hoger dan het modale inkomen. Dat komt door een kleine groep met hele hoge inkomens. Zij verdienen zoveel, dat ze daarmee het gemiddelde beïnvloeden. Het gemiddelde inkomen zegt dus niet zoveel over het inkomen van een doorsnee persoon. Daarvoor kun je beter naar Jan Modaal kijken.
Mediaan
Als je getallen op volgorde staan, dan is de mediaan het middelste getal. In een oneven reeks is de mediaan precies het getal dat in het midden ligt. Bestaat je getallenreeks uit een even aantal getallen, dan is er geen middelste getal en is de mediaan het gemiddelde van de twee getallen in het midden van je cijferreeks.
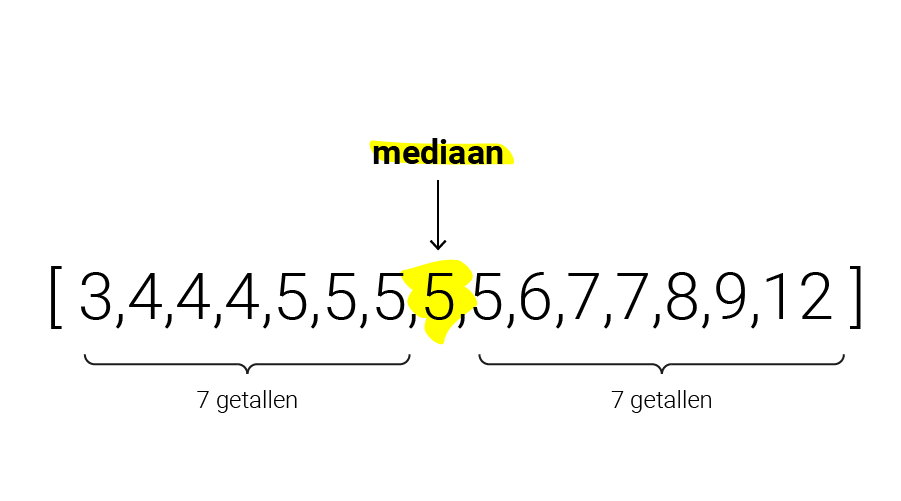
Dit is bij onze cijferreeks nog goed te doen, want je kunt het overzicht makkelijk behouden. Als je reeks uit een honderd-miljoen-miljard cijfers bestaat, kun je de mediaan als volgt berekenen:
De uitkomst van deze som is de plek waar je de mediaan kunt vinden in je cijferreeks. Als de uitkomst geen heel getal is, dan neem je het rekenkundig gemiddelde van de dichtstbijzijnde hele getallen.
De mediaan staat in onze volgorde op de achtste positie.
De mediaan zegt iets over hoe de getallen verdeeld zijn: de helft van de getallen zit erboven, de andere helft van de getallen zit eronder. Waar we eerder zagen dat het rekenkundig gemiddelde wordt beïnvloed door uitschieters, is de mediaan een stuk stabieler.
tl;dr
Mediaan
De mediaan is het middelste getal in je getallenreeks en verdeelt je reeks in twee groepen van evenveel getallen.
Kwartielen
Je kunt de gegevens nog verder verdelen, door de mediaan-berekening nog een keer toe te passen op allebei de helften. Daarmee verdeel je de data in vier gelijke groepen - zogenoemde kwartielen.
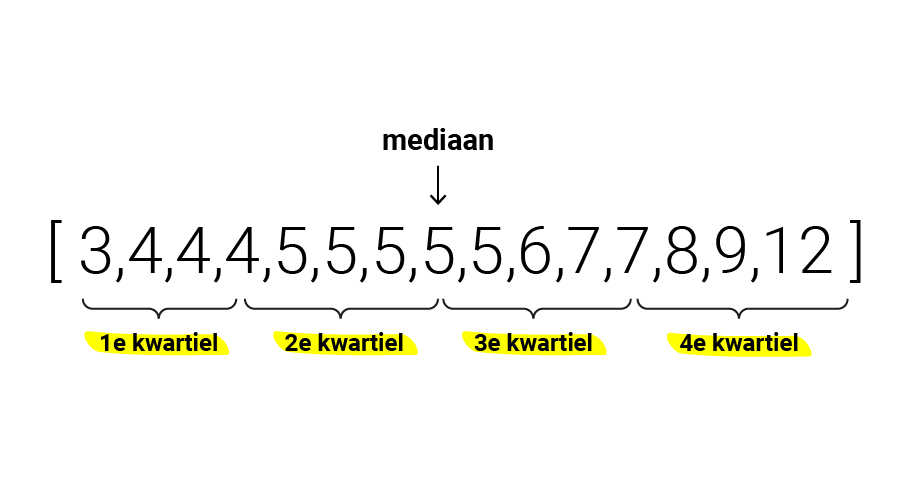
Doordat je weet hoe de getallen verdeeld zijn, kun je inmiddels een aantal zinnige dingen zeggen over de getallenreeks:
je kent de uitersten: minimum en maximum
je kent het rekenkundig gemiddelde
je weet welk getal het vaakst voorkomt, de modus
je kunt iets zeggen over de verdeling van de cijfers met behulp van de mediaan en de kwartielen
Boxplot
Wil je helemaal grip krijgen op de cijfers, dan kun je ervoor kiezen om je cijfers in beeld te brengen. Dat kan met een boxplot, een visuele weergave van de verdeling van je gegevens. Een boxplot tekenen is heel eenvoudig: eerst bereken je het minimum en het maximum.
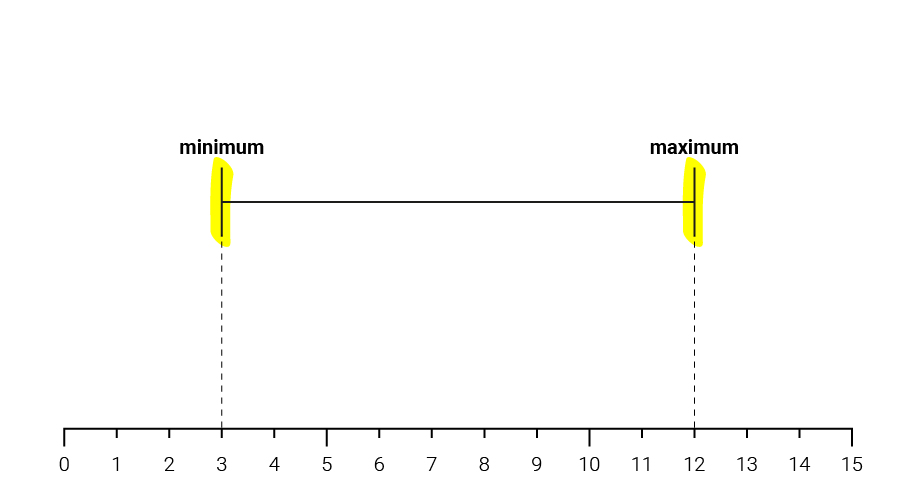
Daarna teken je de mediaan en de kwartielen. Van de middelste kwartielen maak je een rechthoek.
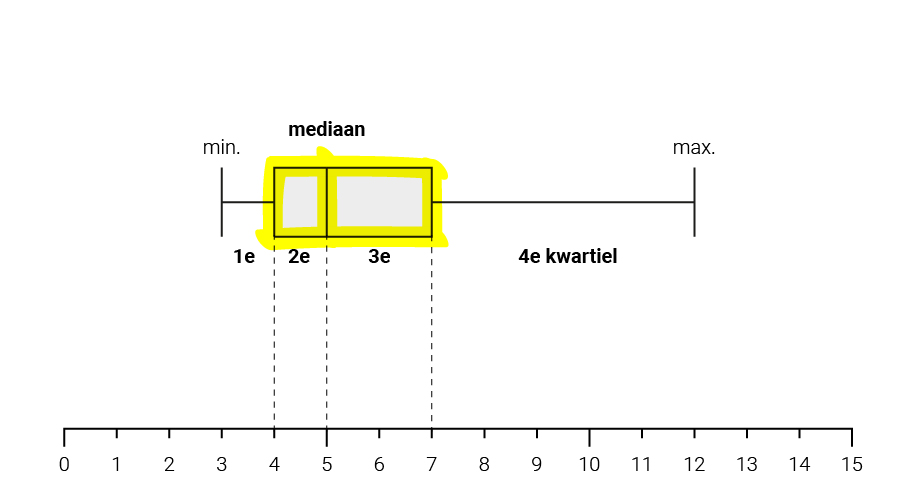
Voilá! Je visuele samenvatting is af. Je ziet nu goed hoe de gegevens verdeeld zijn:
De mediaan verdeelt de cijfers in een ‘hoogste helft en een laagste helft’.
Het rechthoek laat het centrum zien: de middelste 50% van de getallen.
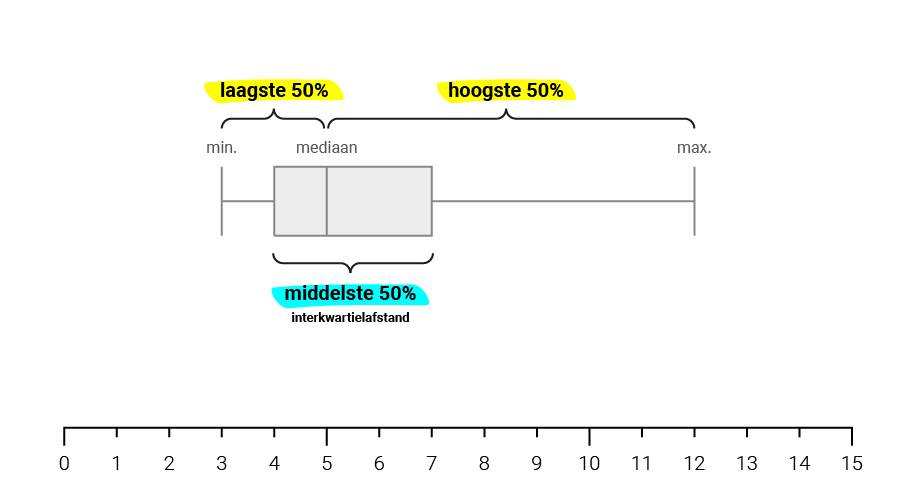
Naast dat een boxplot een handige visuele samenvatting van je gegevens is, kun je aan de vorm ook goed afleiden wat relevant is.
In eerste instantie ging je aandacht misschien uit naar die ene twaalf, omdat dat de grootste uitschieter is. Maar aan de vorm van je boxplot kun je zien dat de meerderheid van de getallen een stuk lager is. Sterker nog, we weten dat de helft van de gegevens bestaat uit vieren en vijven. Die zijn journalistiek gezien misschien wel relevanter dan die ene twaalf. Na Prinsjesdag berichten media bijvoorbeeld over wat de veranderingen voor modale huishoudens betekenen. Berichten over het effect voor de één procent rijkste huishoudens zijn dan veel schaarser.
tl;dr
Boxplot
Een boxplot is een visuele samenvatting van een dataset: de grafiek laat zien hoe de getallen verdeeld zijn.
Als je als journalist met cijfers werkt, wil je zeker weten dat je de getallen goed begrijpt. Om Babylonische spraakverwarringen te voorkomen, leggen we je uit hoe de wetenschappelijke notatie werkt en wat het verschil is tussen de korte en de lange schaal.
Wetenschappelijke notatie
Omdat wetenschappers vaak met heel grote of juist heel kleine getallen werken, hebben ze een andere manier bedacht om getallen op te schrijven. Met de wetenschappelijke notatie is het verschil tussen vier miljoen en vier miljard in een oogopslag duidelijk. Wanneer je vier miljoen uitschrijft gebruik je zes nullen: 4.000.000. Voor vier miljard gebruik je negen nullen: 4.000.000.000. Door de wetenschappelijke notatie te gebruiken, zijn de twee getallen makkelijker te onderscheiden en hoef je niet al die nullen op te schrijven.
Wetenschappers gebruiken de macht van tien om dit soort getallen op te schrijven. Bij een macht van tien is de exponent gelijk aan het aantal nullen. Anders gezegd: de exponent geeft aan hoeveel plaatsen de komma naar rechts opschuift en dus hoeveel nullen erbij komen als je het getal wel wilt uitschrijven. Vier miljoen, een vier met zes nullen, wordt 4x106. Hierbij is zes de exponent. Vier miljard, een vier met negen nullen, wordt 4x109. Soms gebruikt de wetenschap een · in plaats van een x-teken; maar 4x109 en 4·109 betekenen hetzelfde.
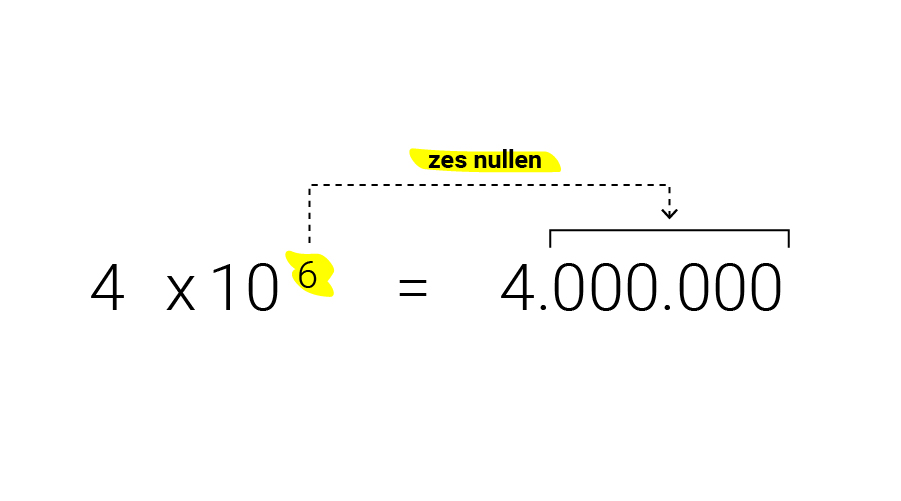
Bij heel kleine getallen gebruiken wetenschappers een negatieve exponent. Dan geeft de exponent aan hoeveel nullen er links bijkomen - met één nul voor de komma. Met 4x10-2 praat je over vier honderdste en schrijf je 0,04.
De lange en korte schaal
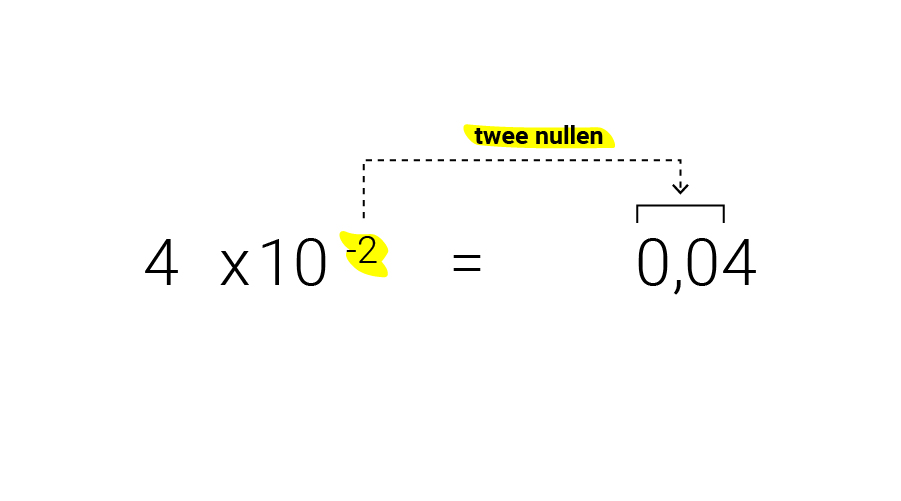
Behalve de wetenschappelijke notatie, bestaan er nog twee manieren voor het opschrijven van grote getallen: de korte en de lange schaal. In Nederland gebruiken we de lange schaal. Als we het over grote getallen hebben, dan praten we vaak over miljoenen (106), miljarden (109), biljoenen (1012), en biljarden (1015). Bij elke stap omhoog komen er drie nullen bij, en bij elke stap terug gaan er drie nullen af.
Een miljard is dus duizend miljoen; een biljard is duizend biljoen; en honderd-miljoen-miljard is honderd biljard of tienduizend biljoen.
In de Verenigde Staten en Groot-Brittannië wordt de korte schaal gebruikt. Dit betekent dat ze daar de treden die eindigen op -ard overslaan. Als ze het daar over grote getallen hebben, dan volgt na een miljoen (106), een biljoen (109), en een triljoen (1012). In de vaak Engelstalige landen die de korte schaal gebruiken, is een 'billion' dus een Nederlands miljard. Een vergissing is snel gemaakt, dus let goed op: in het Nederlands heeft een biljoen twaalf nullen en een miljard negen nullen. Een Engelse billion heeft negen nullen, en is dus gelijk aan een Nederlands miljard. Een ongeluk schuilt in een klein hoekje en in een groot getal; daarom hieronder een overzicht van de korte schaal, de lange schaal, en welke getallen daar bij horen - inclusief de wetenschappelijke notatie.
Ondanks deze tabel zal dit nog honderd-miljoen-miljard keer fout gaan... Godmiljaar.
Zoals Bill Kovach en Tom Rosenstiel beschrijven in The Elements of Journalism, is de eerste taak van nieuwsjournalisten om “te verifiëren welke informatie betrouwbaar is, en deze dan te ordenen zodat mensen de informatie gemakkelijk kunnen begrijpen”. Voor journalisten die werken met cijfers, betekent dit dat de nummers waar ze van zijn gaan houden, misschien niet in de uiteindelijke productie thuis horen.
Afronden
Vanzelfsprekend moet je precies en nauwkeurig werken als je cijfers gebruikt voor journalistieke verhalen. Maar om ervoor te zorgen dat het publiek jouw verhaal gemakkelijk kan begrijpen, wil je die precisie in de uiteindelijke publicatie misschien wel beperken. Zo kun je ‘41,812 procent van de bevolking’ misschien beter op schrijven als ‘zo'n 4 op de 10 mensen’. In onze ervaring is de juiste mate van precisie ongeveer gelijk aan de precisie die je zou gebruiken als je over je verhaal vertelt aan niet-data-nerd-vrienden op een zaterdagmiddag.
Het is waar dat ‘41,812 procent’ preciezer is, maar welke waarde voegt deze nauwkeurigheid toe? De uiteindelijke journalistieke productie wordt niet per se beter leesbaar of eenvoudiger te begrijpen; en ‘zo'n 4 op de 10 mensen’ is niet onjuist. Bovendien kún je vaak een cijfer helemaal niet zo precies weten, dus dan is een te precies cijfer ook nog eens misleidend. Daarbij heeft goede journalistiek het (valse?) gevoel van precisie en nauwkeurigheid dat decimalen met zich meebrengen niet nodig: goede journalistiek is precies en nauwkeurig - dat kan ook zonder decimalen. Dat gezegd hebbende is de titel van deze website natuurlijk gekscherend gekozen: vriendelijk zijn voor je publiek door ‘4 op de 10 mensen’ op te schrijven, ontslaat je niet van de plicht de cijfers te controleren op juistheid.
Beperken
Het aantal cijfers dat je noemt in een uiteindelijke publicatie, wil je misschien beperken. Vaak communiceert een infographic beter dan een rits cijfers. Kortom: wees terughoudend met het gebruik van cijfers in je tekst. In het algemeen kun je stellen dat het gebruik van meer dan drie cijfers in één alinea al aan de hoge kant is (uitzonderingen daargelaten).
Uitschrijven
Hoewel het per medium kan verschillen - raadpleeg bij twijfel altijd het stijlboek van desbetreffend medium - geldt in het Nederlands in het algemeen dat ronde getallen zoals veertig, vijftig, honderd en getallen tot en met vijfentwintig worden uitgeschreven. Daarom schreven wij eerder het volgende over de PvdA verkiezingsuitslagen uit 2012 en 2017: “Maar ook de verandering - de val van 38 naar negen zetels - heeft nieuwswaarde.”
Op sommige momenten schrijf je cijfers niet uit; bijvoorbeeld bij leeftijden, jaartallen, maten, geldbedragen en percentages. Let wel op dat je in de lopende tekst geen %-teken gebruikt maar procent uitschrijft.
Nieuwe kennis beklijft door gebruik. Deins de volgende keer dus niet terug voor een verhaal met cijfers: het is een kans om alles wat je hier leerde, toe te passen. Wij zouden nog wel even door kunnen praten over cijfers, maar dit was het voor nu: opvoeden is ook een kwestie van loslaten.
Mocht je echt de smaak te pakken hebben en meer willen leren, dan zijn spreadsheets een goede start. Volgens de Amerikaanse datajournalist Steve Doig kun je “negentig procent van alle datajournalistieke verhalen maken met Excel”.
Alle sommen en berekeningen die op Als Het Ongeveer Maar Klopt langs kwamen, kun je eenvoudig reproduceren in een spreadsheet-programma zoals Microsoft Excel of Google Spreadsheets.
Als je deze berekeningen wilt doen met behulp van Microsoft Excel of Google Spreadsheets, moet je zogenoemde ‘functies’ gebruiken. In beide programma's beginnen functies met het =-teken; gevolgd door de naam van de functie en de benodigde ingrediënten. Met een functie laat je de computer weten, dat je wilt dat de computer iets voor je uitrekent. De opdracht, wat de computer precies uitrekent, zit besloten in de naam van de functie. Alles wat de computer nodig heeft om dat uit te rekenen, staat tussen de haken.
Niet alleen bestaan er verschillen tussen functies in Google Spreadsheets en Microsoft Excel; er zijn bij beide programma's ook verschillen tussen de Engelstalige en Nederlandstalige versies. Daarom hieronder een overzicht met de functies die horen bij de berekeningen die je op Als Het Ongeveer Maar Klopt langs zag komen: een tabel met functies in het Nederlands en Engels voor Excel, en nog zo'n tabel voor Google Spreadsheets.
In onze ervaring dragen te veel journalisten ‘niet kunnen rekenen’ als een medaille op de borst. Alsof eenvoudig te overkomen onkunde een prestatie is, waar je trots op moet zijn. Daar snappen wij dus niets van: journalisten die niet kunnen of willen rekenen, zijn makkelijk te misleiden.
Omdat creëren altijd beter is dan klagen, besloten we zelf aan een antwoord te gaan werken. Dat voornemen resulteerde in Als Het Ongeveer Maar Klopt: een korte online gids om journalisten cijferwijzer te maken.
Zonder koffie en nerd-humor was deze site er niet gekomen. Maar behalve elkaar, willen we graag Hugo van der Parre bedanken voor de onbewuste titelsuggestie; Daniël Verlaan voor de single page inspiratie; en Sanne Blauw omdat we de term ‘cijferwijzer’ voor het eerst in haar nieuwsbrief lazen. Hoofdstuk twee is geïnspireerd door het boek ‘Cijfers in het Nieuws’ door Willem Koetsenruijter en Rinke Berkenbosch; en hoofdstuk vier is deels gebaseerd op Winny’s essay voor het Data Journalism Handbook. Verder maakt deze website dankbaar gebruik van de volgende open bronnen:
En uiteraard willen we jou bedanken. Wilde plannen en ideeën worden pas echt waardevol in de uitvoering. Wij hopen dat ten minste een paar mensen cijferwijzer worden door AHOMK. Wellicht ben jij er een van - dank voor je aandacht en je tijd. We zouden het tof vinden als je anderen over deze site vertelt of als je ons een pizzapunt cadeau doet.
Dankje. Laters!
Lars en Winny
Over de makers
Lars Boogaard werkt als infographicmaker bij Nieuwsuur. Eerder werkte hij bij NOS op 3, waar hij interactieve klikdingen en dataplaatjes maakte voor leeftijdsgenoten. In zijn vrije tijd zit hij aan de buis gekluisterd voor zo’n beetje elke sportwedstrijd. En zit 'ie niet achter de tv, dan wel op z’n racefiets. Soms fietst hij dan naar koffiezaken om daar aan sterk werkgerelateerde websites te klussen. Ontspannen kan altijd nog - met Mad Man bijvoorbeeld.
Wanneer Winny de Jong niet bij de NRC aan het werk is; dan leest, schrijft of denkt ze wel over haar vak. Zo verzamelt ze elke week het beste van het datajournalistieke web in haar Engelstalige nieuwsbrief. Naast werk heeft ze ook andere hobby's: zo leert ze salsa dansen en sport ze graag.
07 Vrienden
We hielden een niet-representatieve steekproef onder slimme mensen die aardige dingen zeiden over Als Het Ongeveer Maar Klopt.
review
“Bondig, overzichtelijk en luchtig: dit past in de traditie van het beste datajournalistieke onderwijs!”
Luuk Sengers, datajournalist en datatrainer
review
“Wat een goed idee en wat goed uitgevoerd!”
Ionica Smeets, hoogleraar wetenschapscommunicatie
review
“Deze site is zeer goed opgebouwd! Leerzaam in gemakkelijke stappen en fijn van toon, vooral niet belerend.”
Pim Peterse, Bureau van Lokale Zaken
review
“Deze site is honderd procent goud. Wat een fijne, toegankelijke cijferles - met veel lachsalvo's tussendoor. Echt heel mooi gedaan.”
Roselien Herderschee, freelance journalist
review
“Je hebt leugens, grove leugens en statistieken wordt wel gezegd. Woorden moeten stroken met wat gebeurt, cijfers moeten kloppen. En daar kun je niet genoeg bij geholpen worden.”
André Meinema, financiëel redacteur/verslaggever NOS
review
“Deze site is een mooi initiatief! Ik heb het met veel plezier gelezen.”
